Trabajo Práctico N°2¶
El presente trabajo práctico fue realizado por los alumnos:
- Anarella Nicoletta (Padrón 94551)
- Bruno Grassano (Padrón 103855)
- Ignacio Javier Mermet (Padrón 98153)
- Joaquin Gomez (Padrón 103735)
Ejercicio 1¶
Basándose en los trabajos
- Performance Modelling of Imaging Service or Earth Observation Satellites with Two-dimensional Markov Chain
- Queuing theory application in imaging service analysis for small Earth observation satellites
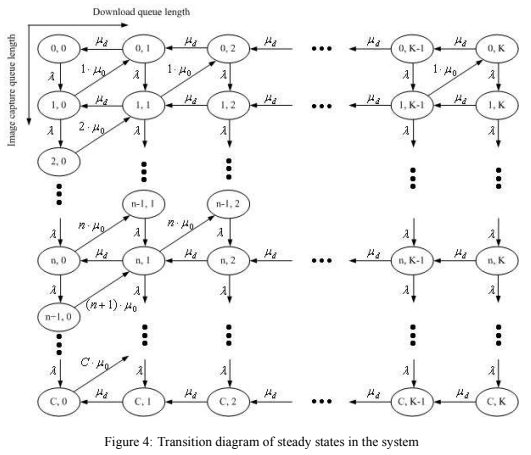
Se pide implementar las soluciones propuestas por los autores utilizando Cadenas de Markov, y Teoría de Colas, considerando:
- Utilizar el generador de números al azar implementado en el Trabajo Práctico 1 para generar los números al azar utilizados en el ejercicio (comparar los resultados con los obtenidos si se utilizan los números al azar provistos por el lenguaje elegido)
- Probar distintos escenarios
- Opcional Comparar los resultados obtenidos, con los resultados que se obtendrían con un Generador Congruencial Lineal de módulo 2 32, multiplicador 1013904223, incremento de 1664525 y semilla igual a la parte entera del promedio de los números de padrón de los integrantes del grupo
class Satellite:
def __init__(self, C=math.inf, K=4, μd=5, μ0=0.5, λ=2, generator = LXM()):
"""Args:
C: Capture queue length limit.
K: onboard storage capacity.
μd: The download service time of an image is assumed exponentially distributed with mean 1/μ_d.
μ0: The basic image capture service time is exponentially distributed with mean 1/μ_0
λ: Arrival rate of new requests.
"""
@property
def onboard_storage_capacity(self):
return self.K
@property
def images_on_onboard_storage(self):
return self.m
@property
def pending_requests(self):
return self.n
def transition(self):
ps = []
nexts = []
if 0 <= self.n < self.C and 0 <= self.m <= self.K:
ps.append(self.λ)
nexts.append((self.n + 1, self.m))
if 0 < self.n <= self.C and 0 <= self.m < self.K:
ps.append(self.n * self.μ0)
nexts.append((self.n - 1, self.m + 1))
if 0 <= self.n <= self.C and 0 < self.m <= self.K:
ps.append(self.μd)
nexts.append((self.n, self.m - 1))
ps = np.array(ps)
p = self.gen.generar() * ps.sum()
try:
self.n, self.m = nexts[np.digitize(p, np.cumsum(ps))]
except:
print(f"nexts={nexts} ps={ps} p={p} ps.cumsum()={ps.cumsum()} n={self.n} m={self.m}")
raise
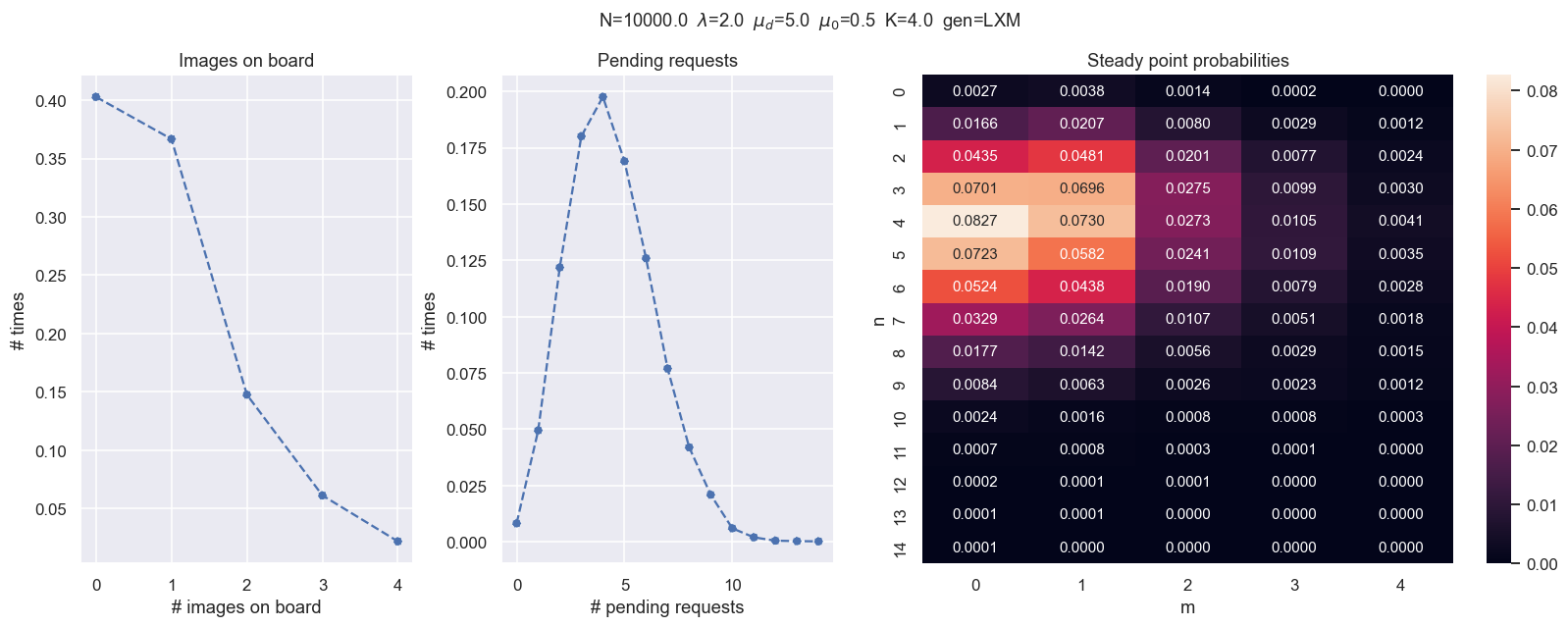
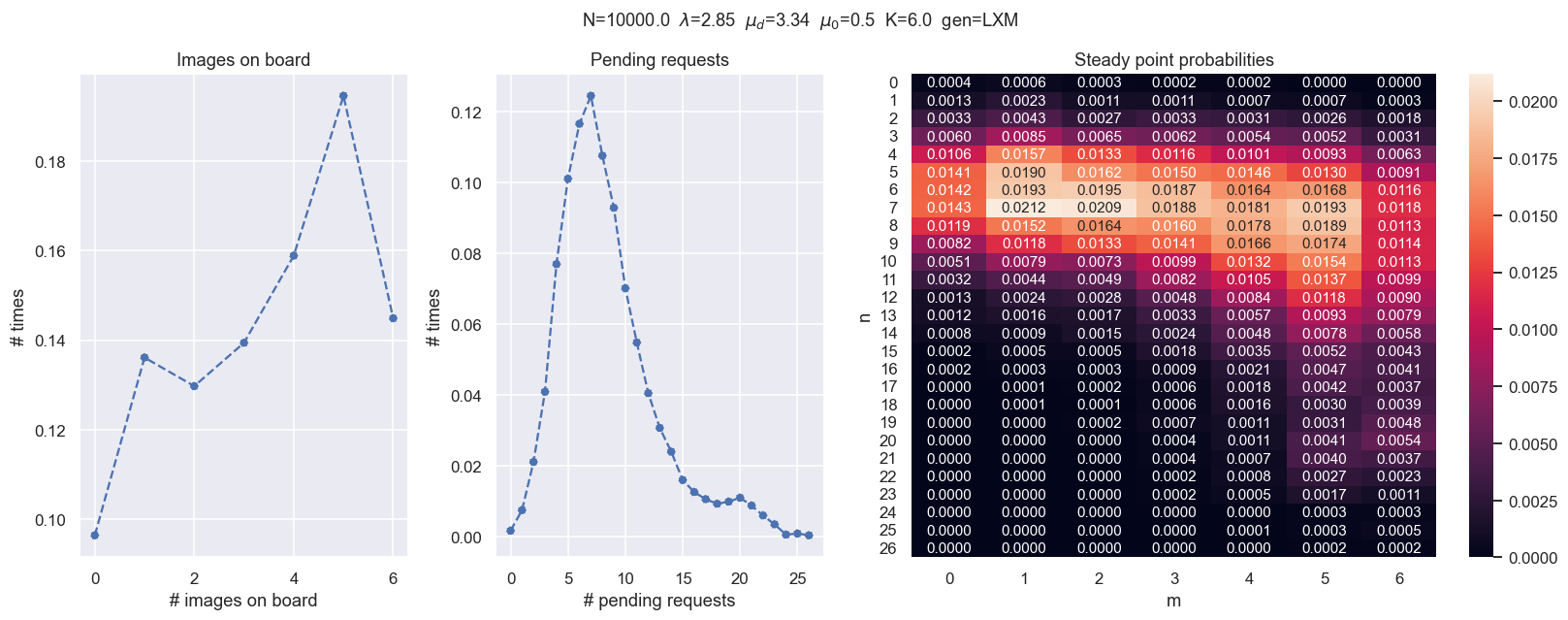
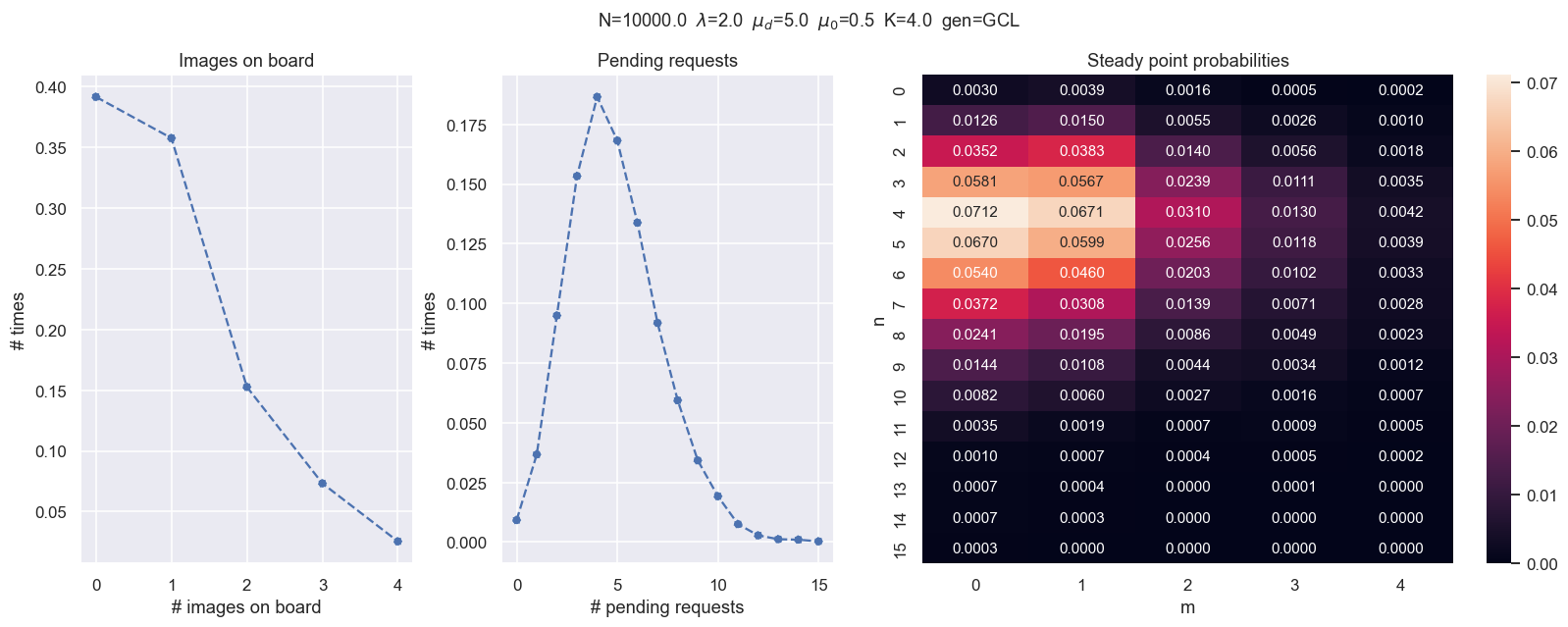
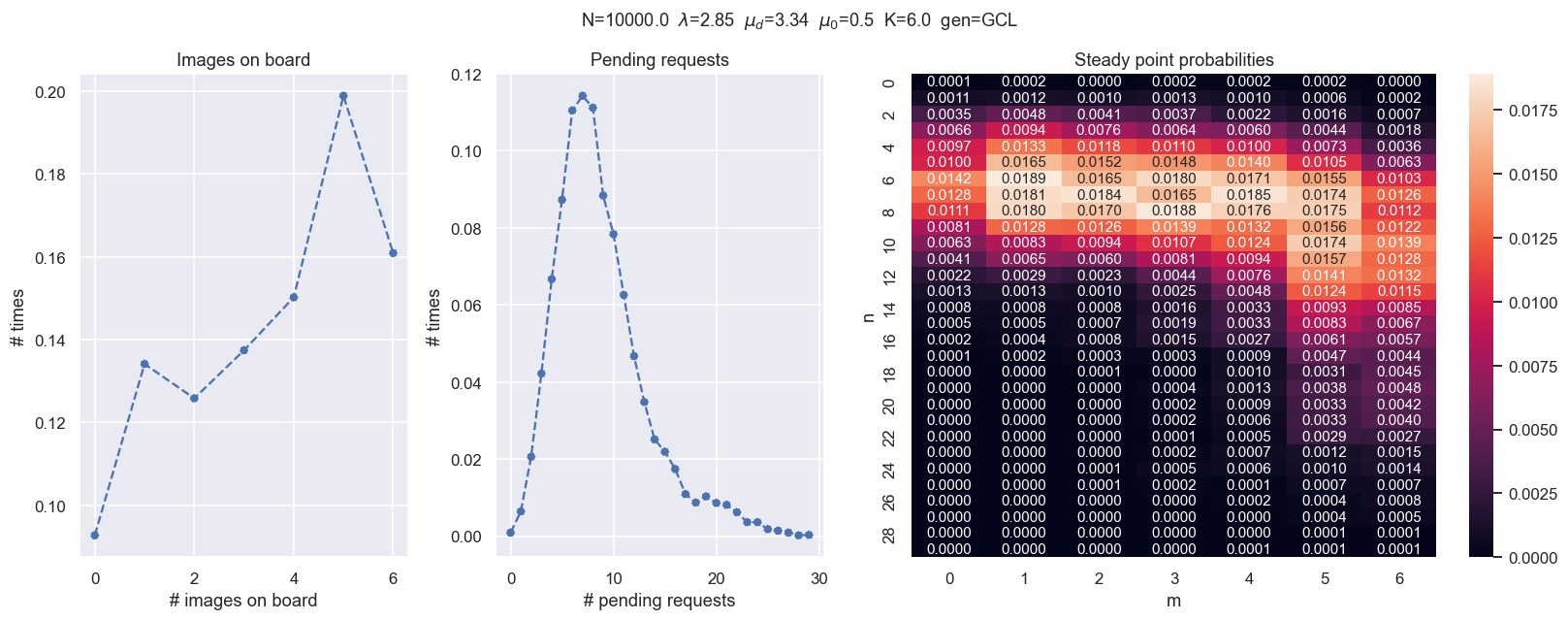
Ejercicio 2¶
Utilizar Simpy para simular una sección del ejercicio 1 a elección
Vamos a necesitar generar valores exponenciales, los obtenemos con la transformada inversa.
def exponencial(lambdaArgumento, generador):
uniforme = generador.generar()
return - np.log(1 - uniforme) / lambdaArgumento
Definimos el modelo del satelite y la solicitud.
class Satelite:
def __init__(self, env, servicioDescarga, lambdaArgumento, generador):
self.env = env
self.lambdaArgumento = lambdaArgumento
self.generador = generador
self.servicioDescarga = servicioDescarga
self.largoColaEnTiempo = []
self.tiemposDeServicio = []
self.tiemposDeServicioAfectadosPorLaCola = []
self.tiempoEntreArribos = []
self.tiemposAcumulados = []
def atencion(self, id):
tiempoAtencion = exponencial(self.lambdaArgumento, self.generador)
servicio = self.servicioDescarga.request()
yield servicio
N = 1
largoCola = len(self.servicioDescarga.queue)
if largoCola != 0:
N = largoCola
tiempoServicio = tiempoAtencion / N
self.largoColaEnTiempo.append(largoCola)
self.tiemposDeServicio.append(tiempoAtencion)
self.tiemposDeServicioAfectadosPorLaCola.append(tiempoServicio)
yield env.timeout(tiempoServicio)
self.servicioDescarga.release(servicio)
class Solicitud:
def __init__(self, env, satelite, id):
self.env = env
self.satelite = satelite
self.id = id
def tratarse(self):
return self.satelite.atencion(self.id)
Creamos la funcion que se va a encargar de generar las solicitudes. Estas son nuevos procesos que van a intentar usar el servicio del satelite.
A medida que van llegando de avanza el tiempo del ambiente.
def generarArribos(lambdaArgumento, generador, cantidadArribos, env, satelite):
tiempoAcumulado = 0
id = 0
while (id < cantidadArribos):
tiempo = exponencial(lambdaArgumento, generador)
nuevaSolicitud = Solicitud(env, satelite, id)
id = 1 + id
env.process(nuevaSolicitud.tratarse())
yield env.timeout(tiempo)
tiempoAcumulado += tiempo
satelite.tiemposAcumulados.append(tiempoAcumulado)
satelite.tiempoEntreArribos.append(tiempo)
Establecemos las configuraciones iniciales y ya podemos simular...
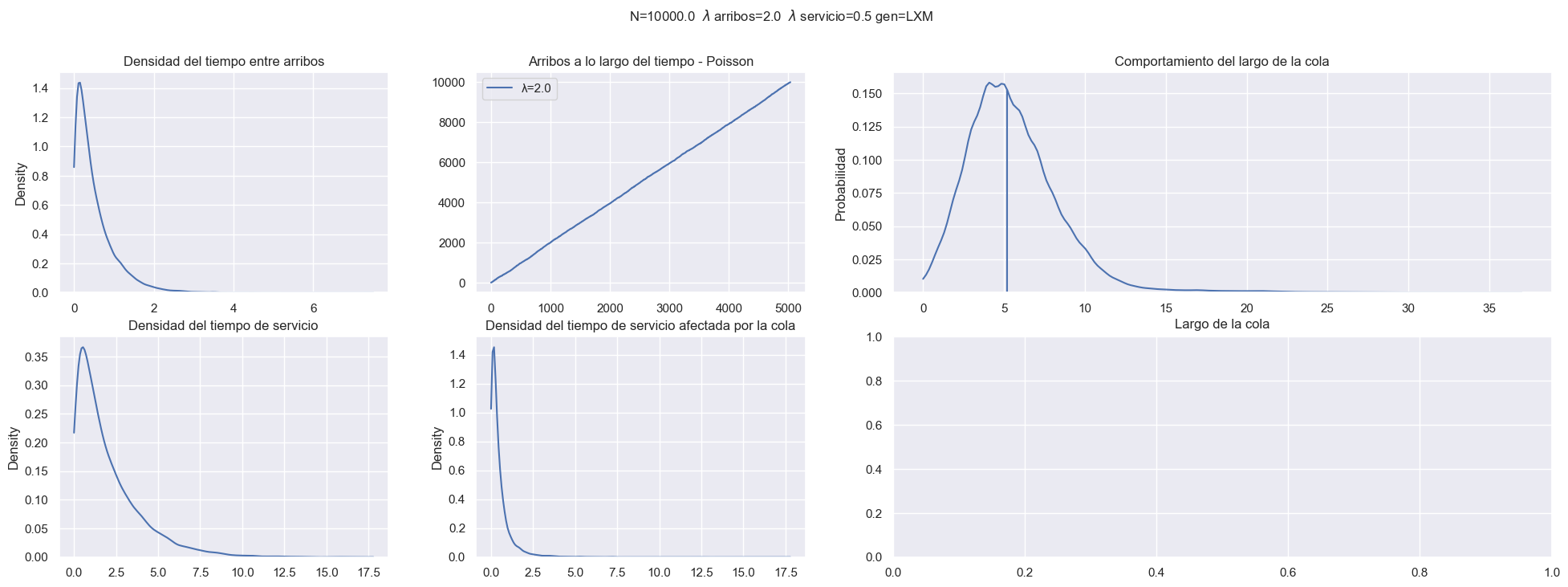
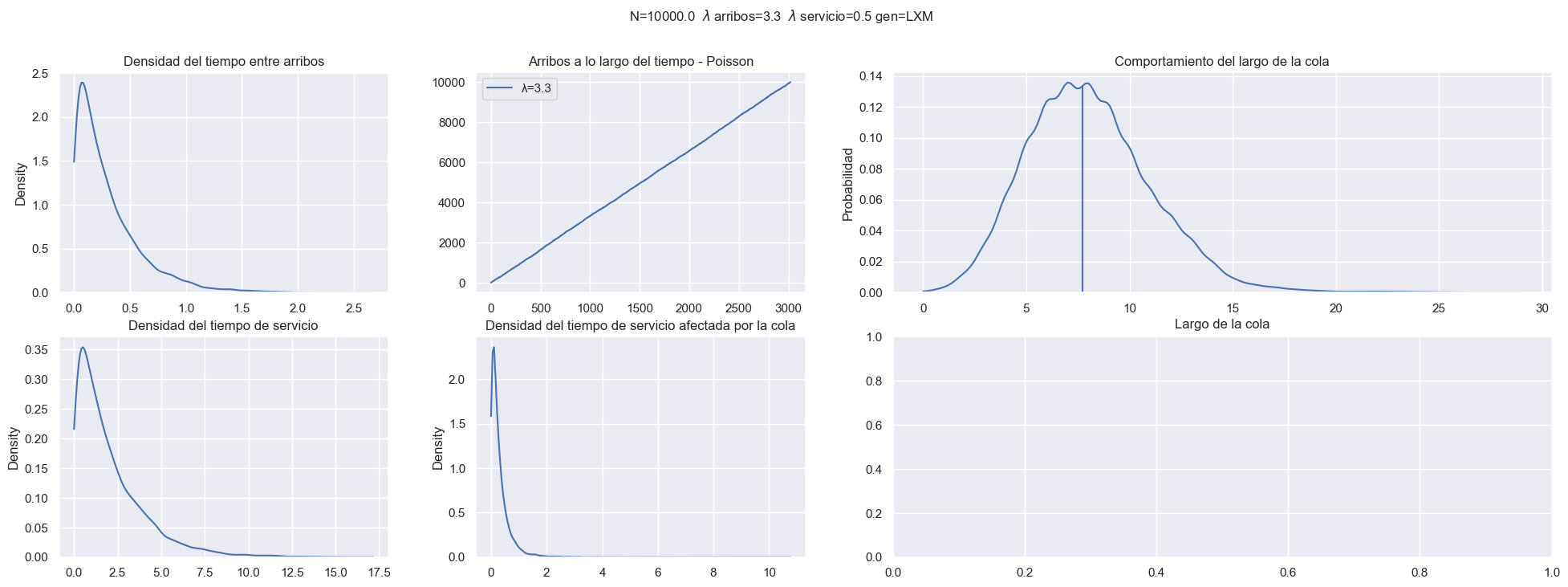
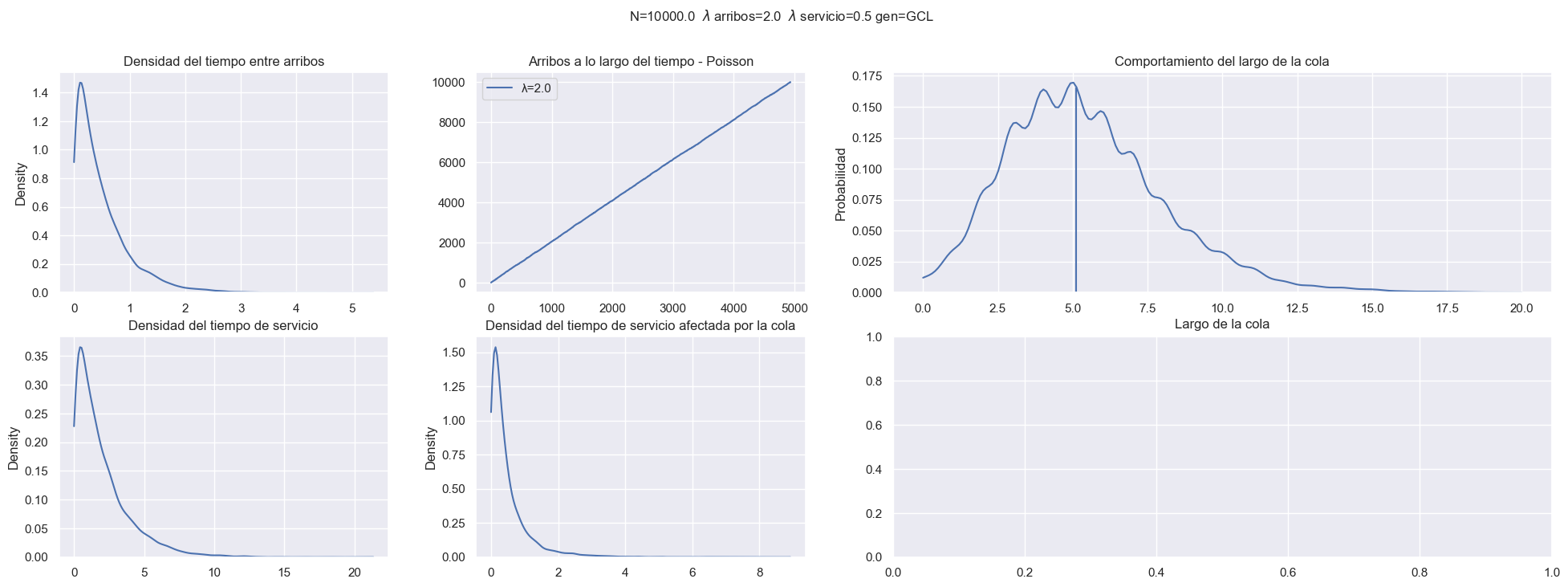
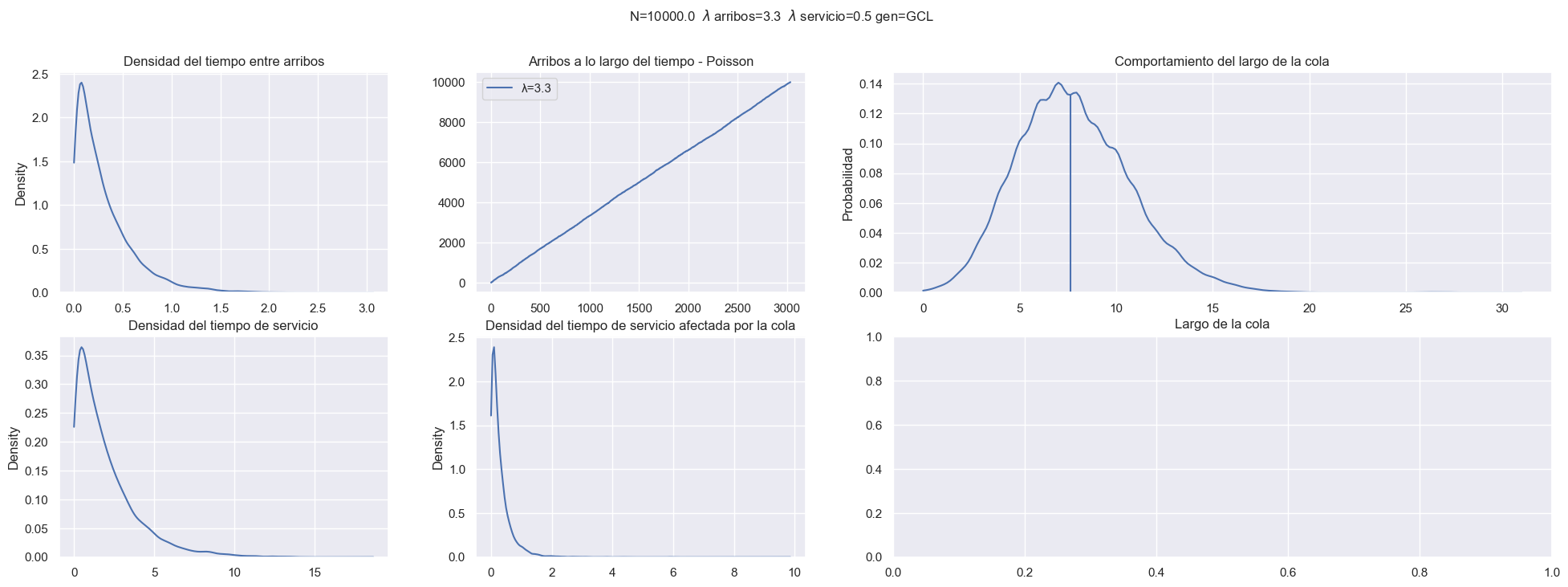
Ejercicio 3¶
Un servidor recibe solicitudes las cuales son procesadas de una por vez en el orden de llegada (política FIFO). Se determinó que en 10 milisegundos existe una probabilidad 𝑝 = 1/40 que llegue una nueva solicitud y una probabilidad 𝑞 = 1/30 que una solicitud termine de ser procesada y deje el sistema. Se desea estudiar la cantidad de solicitudes en el servidor considerando tanto las que están en cola esperando ser procesadas como la solicitud que está siendo procesada.
- Determine la matriz de transición de estados explicando cómo se obtiene la misma.
- Utilizando Matlab, Octave o Python simule la evolución del sistema a lo largo de 1.000 segundos. Suponga que el sistema puede tener como máximo 30 estados posibles y que el servidor comienza sin estar procesando solicitudes.
- Realice un gráfico mostrando la cantidad de solicitudes en el servidor en cada instante de tiempo.
- Realice un histograma mostrando cuantas veces el sistema estuvo en cada estado.
- Determine el % de tiempo que el servidor se encuentra sin procesar solicitudes.
Matriz de transición de estados¶
Para resolver este ejercicio vamos a definir 2 eventos independientes entre sí:
A: arriba al sistema una nueva solicitud
E: una solicitud es procesada y egresa del sistema
Esto nos permitirá descomponer a los estados del servidor dependiendo de cuántas solicitudes se estén procesando. La matriz de transición de estados quedaría entonces:
M = | P0->0 P0->1 P0->2 P0->3 P0->4 ... |
| P1->0 P1->1 P1->2 P1->3 P1->4 ... |
| P2->0 P2->1 P2->2 P2->3 P2->4 ... |
| ... ... ... ... ... ... |Sabemos que:
P(A) = p = 1/40
P(E) = q = 1/30
r = P(~A) = 1-P(A) = 1-1/40 = 39/40
s = P(~E) = 1-P(E) = 1-1/30 = 29/30
Si hay solicitudes pendientes:
- La probabilidad que en el próximo estado haya una solicitud menos es r*q
- La probabilidad que en el próximo estado haya una solicitud más es p*s
- La probabilidad de quedar igual es rs+pq
Si no hay solicitudes pendientes:
- La probabilidad que en el próximo estado haya una solicitud más es p
- La probabilidad de quedar igual es r
Entonces, podemos reescribir la matriz de transición de estados como:
M = | r p 0 0 0 ... |
| r*q r*s+p*q p*s 0 0 ... |
| 0 r*q r*s+p*q p*s 0 ... |
| ... ... ... ... ... ... |Simulación con 1.000 segundos suponiendo que no hay solicitudes por procesar al comienzo¶
N = 1000000 # 1.000 segundos en intervalos de 10 milisegundos
solicitudes_en_proceso = 0
estados = []
for i in range(N):
# Agrego estado a log
estados.append(solicitudes_en_proceso)
# probabilidad de terminar una solicitud en proceso
if solicitudes_en_proceso > 0 and np.random.rand() < 1.0/30:
solicitudes_en_proceso = solicitudes_en_proceso - 1
# probabilidad de que ingrese una solicitud nueva
if np.random.rand() < 1.0/40:
solicitudes_en_proceso = solicitudes_en_proceso + 1
Procedemos a graficar la cantidad de solicitudes en el servidor en función del tiempo.
plt.figure(figsize=(18, 6), dpi=80)
plt.title('Cantidad de solicitudes en proceso en el servidor en función del tiempo'.format(N), size=20)
plt.xlabel('Tiempo')
plt.ylabel('Cantidad de solicitudes en proceso')
plt.plot(estados, linewidth=1.0)
plt.show()
plt.figure(figsize=(18, 6), dpi=80)
plt.title('Cantidad de ocurrencias de cada estado'.format(N), size=20)
plt.xlabel('Estado')
plt.ylabel('Cantidad de ocurrencias')
plt.hist(estados, bins='sturges', linewidth=1.0, )
plt.show()
Procedemos ahora a analizar el tiempo ocioso del servidor, es decir, el porcentaje de tiempo durante el cual no está procesando solicitudes.
tiempo_sin_procesar_solicitudes = len(list(filter(lambda x: x == 0, estados))) / len(estados) * 100
'El porcentaje de tiempo que el sistema pasa sin procesar solicitudes es {:.3f} %'.format(
tiempo_sin_procesar_solicitudes)
'El porcentaje de tiempo que el sistema pasa sin procesar solicitudes es 25.399 %'
Si revisamos desde la teoría de colas, el modelo corresponde con un M/M/1 donde $\lambda=\frac{1}{40}$ y $\mu=\frac{1}{30}$.
Lo pedido corresponde con $P(0)$, donde podemos usar que $P(0) = 1 - \rho = 1 - \frac{1/40}{1/30} = 0,25$, viendo asi que lo practico se acerca a lo teórico.